1. 定义
红黑树(Red - Black Tree)是一种自平衡二叉查找树,但它在二叉查找树的基础上额外添加了一个标记(颜色),同时具有一定的规则,这些规则使红黑树保证了一种平衡,插入,删除和查找的最坏时间复杂度都为O(logn)。它必须满足以下五个性质:
- 每个节点要么是黑色,要么是红色;
- 根节点(根节点即指树尾端NIL指针或NULL节点)是黑色;
- 每个叶子节点(NIL)是黑色;
- 每个红色节点的两个子结点一定都是黑色;
- 任意一个节点到每个叶子节点的路径都包含相同数量的黑节点。
红黑树的统计性能要好于平衡二叉树(AVL树)。因此,红黑树在很多地方都有应用。在Java集合框架中,很多部分(HashMap,TreeMap和TreeSet等)都有红黑树的应用,这些集合都提供了很好的性能。
下图是一棵红黑树:

2. 左旋 / 右旋
红黑树的左旋 / 右旋 操作是为了调整红黑节点结构,转移黑色节点位置,使其在进行插入和删除操作后仍然能满足上述定义中红黑树的五条性质。

a. Node结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public class Node{
int color = RED;
int data;
Node right;
Node left;
Node parent;
public static final int BLACK = 0x1;
public static final int RED = 0x2;
}
|
b. 右旋操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
private void rightRotation(Node p){
if(p != null){
Node l = p.left;
p.left = l.right;
if(l.right != null){
l.right.parent = p;
}
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
|
c. 左旋操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
private void leftRotation(Node p){
if(p != null){
Node r = p.right;
p.right = r.left;
if(r.left != null){
r.left.parent = p;
}
r.parent = p.parent;
if(p.parent == null){
root = r;
}else if(p.parent.left == p){
p.parent.left = r;
}
else{
p.parent.rigth = r;
}
r.left = p;
p.parent = r;
}
}
|
3. 平衡插入
红黑树的平衡插入主要分两步:
- 首先和二叉查找树的插入一样,进行查找比对并插入
- 随后调整结构,保证满足红黑树的状态
- 对节点进行重新调整颜色
- 对不平衡部分进行相关的旋转操作
红黑树的平衡插入是在二叉查找树插入的基础上,为了进行节点平衡,继续做了插入旋转调整操作。
a. 情景1
插入时父节点与父邻节点均为红色 (此处D节点为新插入节点),具体如图所示:

假设节点D为新插入节点。此时其父节点B与父邻节点C均为红色,不满足第四条性质 (每个红色节点的两个子结点一定都是黑色)*,所以只需将B节点与C节点的颜色转换为黑色,同时,将A节点转换为红色。此时A节点的父节点为红色时,则又会出现不满足*第四条性质 *(每个红色节点的两个子结点一定都是黑色)* 的情况,则将A节点作为新的调整点重复上述颜色调整步骤,直至所有节点颜色满足性质。
b. 情景2
父节点为红色,而父邻节点为黑色 (此处D节点为新插入节点),具体如下图所示:
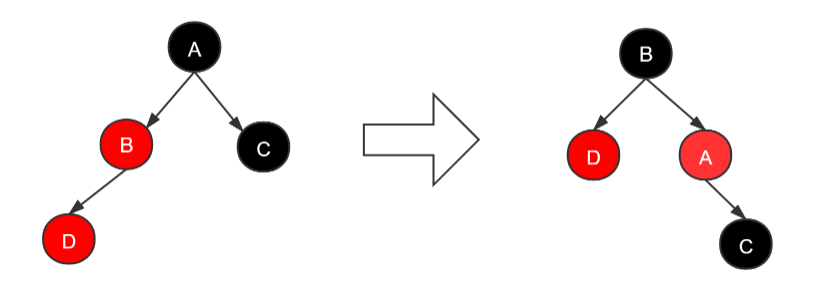
假设节点D为新插入节点,其父节点B为红色,父邻节点C则为黑色,不满足第四条性质 *(每个红色节点的两个子结点一定都是黑色)*,也不能直接改变节点B的颜色为黑色,因为这样将会出现ABC三个节点为黑色,所以只能对A节点进行右旋操作进行平衡。
c. 实例(旋转 + 染色)

- 首先从左侧开始,是一个按照顺序插入生产出来的红黑树,插入顺序;
7、2、8、1、4、3、5
- 向目前红黑树插入元素6,插入后右下角有三个红色节点;
3、5、6。
- 因为右下角满足染色条件,变换后;黑色节点(3、5)、红色节点(4、6)。
- 之后看被红色连线链接的节点
7、4、2,最小节点在中间,左旋平衡树结构。
- 左旋完成后,红色连接线的
7、4、2左倾,因此需要做右旋操作。
- 左旋、右旋,调整完成后,又满足了染色操作。至此恢复红黑树平衡。
4. 平衡删除

红黑树的删除只会面临上述三种情况,删除本身并不复杂。重点难点是在删除的同时要调整其结构,使之继续保持平衡。
a. 情景1
当前节点为左节点,节点B为最终要删除的节点。

其兄弟节点C为黑色,且有一个右节点,下述操作将删除B节点且对其进行调整。
- 将节点B的父节点A的颜色传递给兄弟节点C
- 将父节点A与兄弟节点C的右节点D设置为黑色
- 最终对父节点A进行左旋转,得到最终结果
至此,节点平衡修复结束,因为经过上述修复,均满足红黑树的五条性质。
b. 情景2
当前节点为左节点,节点B为最终要删除的节点。

兄弟节点C是黑色的,且有一个左节点,下述操作将进行调整树结构,随后删除B节点。
- 将兄弟节点C的左节点D设置为黑色
- 将兄弟节点C设置为红色
- 对其兄弟节点C进行右旋
- 回到情景1进行处理
回到情景1进行处理计科再次进行调整删除。
c. 情景3
当前节点为左节点,节点B为最终要删除的节点。
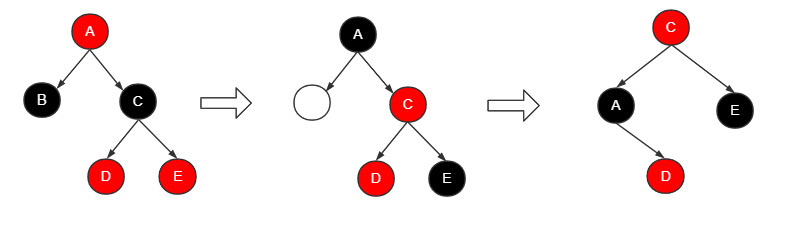
兄弟节点C是黑色的,且有两个节点。
- 将父节点A的颜色赋值给兄弟节点C
- 将兄弟节点C的右子节点E设置为黑色
- 将父节点A设置为黑色
- 删除节点B
- 对父节点A进行右旋操作
至此,该段红黑树已满足性质4 (每个红色节点的两个子结点一定都是黑色) 与性质5 (任意一个节点到每个叶子节点的路径都包含相同数量的黑节点) 。
d. 情景4
当前节点为左节点,节点B为最终要删除的节点。
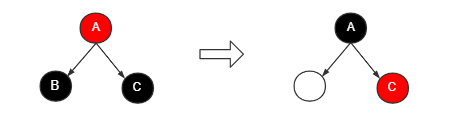
兄弟节点C是黑色的,且没有子节点。
- 将兄弟节点C设置为红色
- 删除节点B
- 将父节点A设置为当前节点并进行递归调整。
直至调整至根节点或遇到红色节点。
e. 情景5
当前左节点B为最终要删除的节点。

兄弟节点C是红色的,且有两个子节点。
- 将兄弟节点C调整为黑色
- 将兄弟子结点D调整为红色
- 删除节点B
- 对父节点A进行左旋操作
至此,该段红黑树已满足性质4 (每个红色节点的两个子结点一定都是黑色) 与性质5 (任意一个节点到每个叶子节点的路径都包含相同数量的黑节点) 。
f. 情景6
当前右节点C是最终要删除的节点。
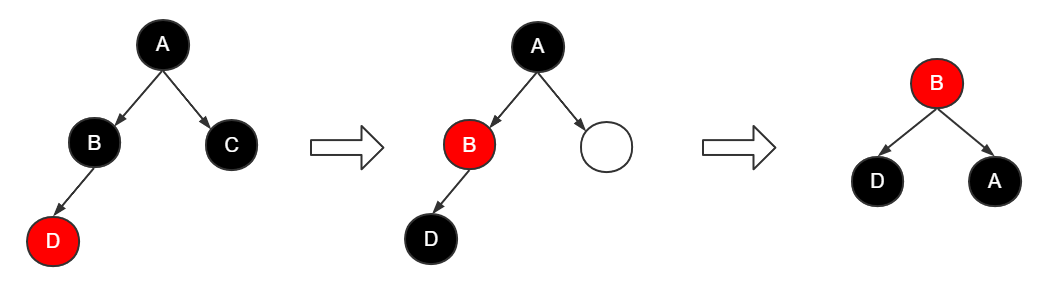
其兄弟节点B为黑色,且有一个左节点。
- 将父节点A的颜色复制给兄弟节点B
- 将父节点A和兄弟节点B的左节点D都设置为黑色
- 删除节点C
- 对父节点A进行右旋操作
至此,该段节选的红黑树部分已满足其性质要求。
g. 情景7
当前右节点C是最终要删除的节点。

其兄弟节点B为黑色,且有一个右节点D。
- 将该右节点D设置为黑色
- 将兄弟节点B设置为红色
- 对兄弟节点B进行左旋操作
随后得到与情景6相同红黑树结构段。
h. 情景8
当前右节点C为最终要删除的节点。
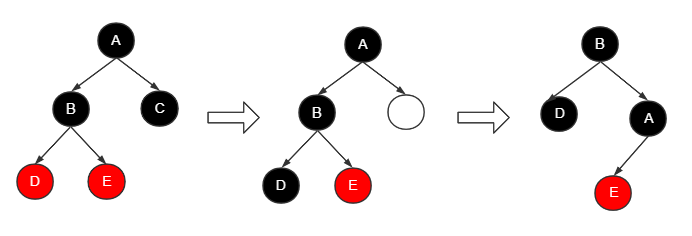
其中兄弟节点B为黑色,同时存在着两个子节点(节点D与节点E)。
- 将父节点A的颜色赋值给兄弟节点B
- 将兄弟节点B的左节点D设置为黑色
- 将父节点A设置为黑色
- 删除节点C
- 对父节点A进行右旋操作
至此,完成平衡删除,得到一段满足性质的红黑树。
i. 情景9
当前右节点C为最终要删除的节点。
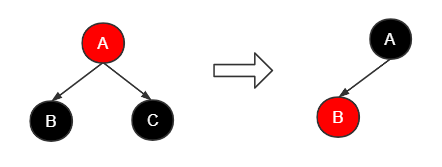
兄弟节点B为黑色,且没有子节点。
- 将兄弟节点B设置为红色
- 删除节点C
- 将父亲节点A设置为当前节点进行递归调整
由父节点A进行递归调整直至根节点或遇到红色节点。
j. 情景10
当前右节点C为最终要删除的节点。
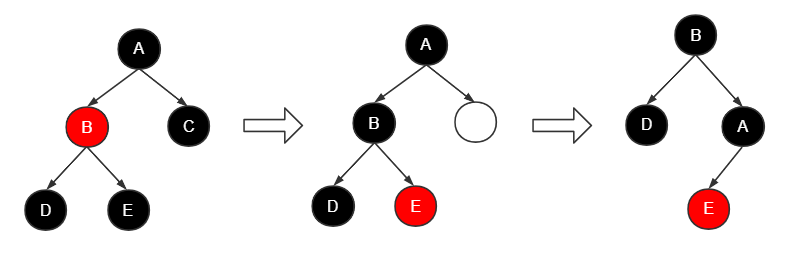
兄弟节点B为红色,且有两个黑色的子节点。
- 将兄弟节点B设置为黑色
- 将兄弟节点B的右子节点E设置为红色
- 删除右节点C
- 对父节点A进行右旋操作
至此,得到的部分树段满足红黑树的性质。
g. 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
|
private void deleteLeafFix(Node deletedNode){
while((deletedNode != root) && (BLACK == deletedNode.color)){
Node parent = deletedNode.parent;
Node brother = getBrother(deletedNode);
if(deletedNode.key.compareTo(parent.key) > 0){
if(RED == brother.color){
brother.color = BLACK;
brother.right.color = RED;
rightRotation(parent);
break;
}else{
if((null == brother.left) && (null == brother.right)){
brother.color = RED;
deletedNode = parent;
}else{
if((null != brother.left) && (RED == brother.left.color)){
brother.color = parent.color;
parent.color = BLACK;
brother.left.color = BLACK;
rightRotation(parent);
break;
}else{
brother.right.color = BLACK;
brother.color = RED;
leftRotation(brother);
}
}
}
}else{
if(RED == brother.color){
brother.color = BLACK;
brother.left.color = RED;
leftRotation(parent);
break;
}else{
if((null == brother.left) && (null == brother.right)){
brother.color = RED;
deletedNode = parent;
}else{
if((null != brother.right) && (RED == brother.right.color)){
brother.color = parent.color;
parent.color = BLACK;
brother.right.color = BLACK;
leftRotation(parent);
break;
}else{
brother.left.color = BLACK;
brother.color = RED;
rightRotation(brother);
}
}
}
}
}
deletedNode.color = BLACK;
}
private Node getBrother(Node node){
if(null == node){
return null;
}
Node parent = node.parent;
if(null == parent){
return null;
}
if(node.key.compareTo(parent.key) > 0){
return parent.left;
}else{
return parent.right;
}
}
public boolean delete(K key){
if(null != key){
if(null != root){
return deleteNode(key, root, null);
}
}
return false;
}
private boolean deleteNode(K key, Node current, Node parent){
if(null != current){
if(key.compareTo(current.key) > 0){
return deleteNode(key, current.right, current);
}
if(key.compareTo(current.key) < 0){
return deleteNode(key, current.left, current);
}
if(key.compareTo(current.key) == 0){
if((null != current.left) && (null != current.right)){
dleTwoChildrenNode(current);
return true;
}else{
if((null == current.left) && (null == current.right)){
deleteLeafFix(current);
if(current.key.compareTo(parent.key) > 0){
parent.right = null;
}else{
parent.left = null;
}
return true;
}else{
dleOneChildNode(current);
return true;
}
}
}
}
return false;
}
private void dleOneChildNode(Node delNode){
Node replaceNode = (null == delNode.left) ? delNode.right : delNode.left;
deltetLeafNode(delNode, replaceNode);
}
private void dleTwoChildrenNode(Node target){
Node replaceNode = successor(target);
if((null == replaceNode.right) && (null == replaceNode.left)){
deltetLeafNode(target, replaceNode);
}else{
target.key = replaceNode.key;
target.value = replaceNode.value;
dleOneChildNode(replaceNode);
}
}
private void deltetLeafNode(Node target, Node replaceNode){
target.key = replaceNode.key;
target.value = replaceNode.value;
deleteLeafFix(replaceNode);
if(replaceNode == replaceNode.parent.right){
replace.parent.right = null;
}else{
replace.parent.left = null;
}
}
private Node successor(Node node) {
if (node == null){
return null;
}
if (null != node.right) {
Node p = node.right;
while (null != p.left){
p = p.left;
}
return p;
} else {
Node p = node.parent;
Node ch = node;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
|
Author:
zchengb
License:
Copyright (c) 2019-2024 zchengb















